미국동부 | [Euclidea] α단계 문제 1.7의 해법 중 7L 7E 달성 방법…
페이지 정보
작성자bqnrxrk2851 작성일16-09-22 11:53 조회2,533회 댓글0건관련링크
본문
α단계 문제 1.7의 해법 중 7L 7E 를 만족시키는 방법이 상당히 어려워 보입니다.
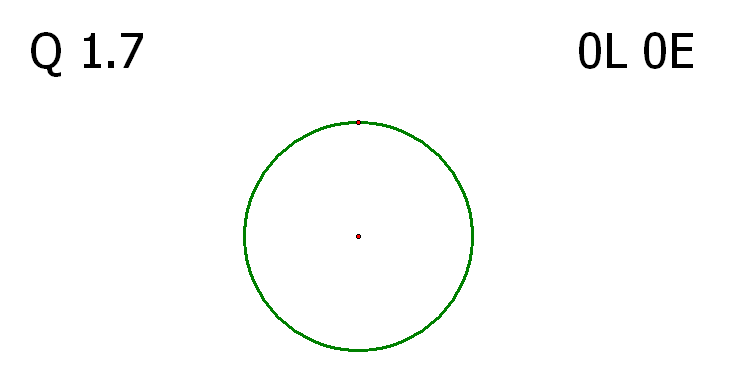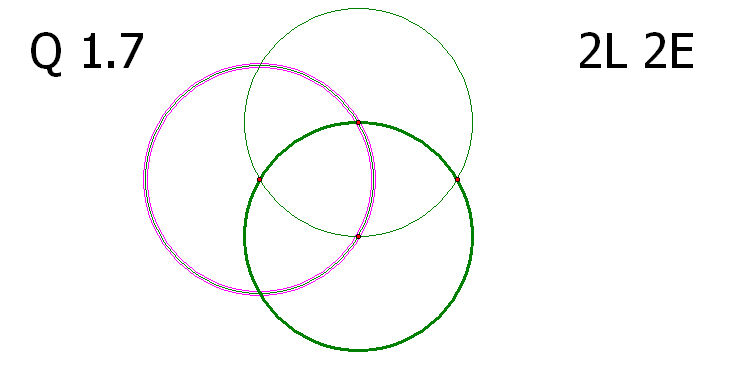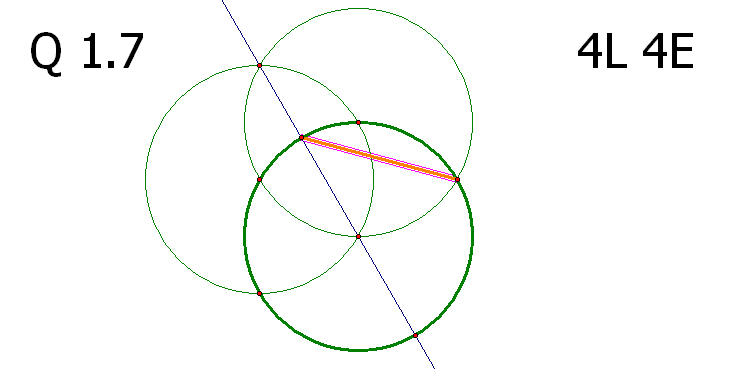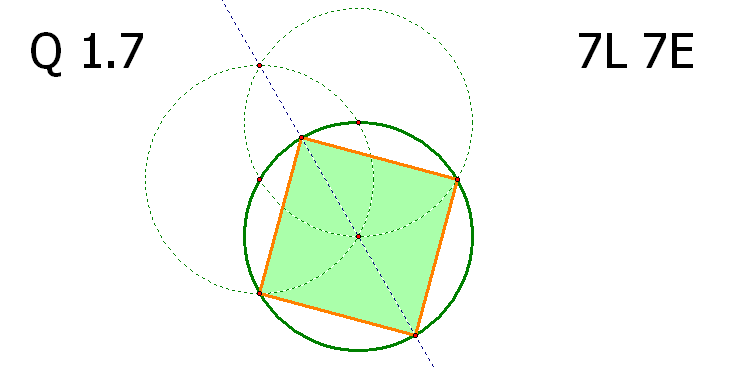
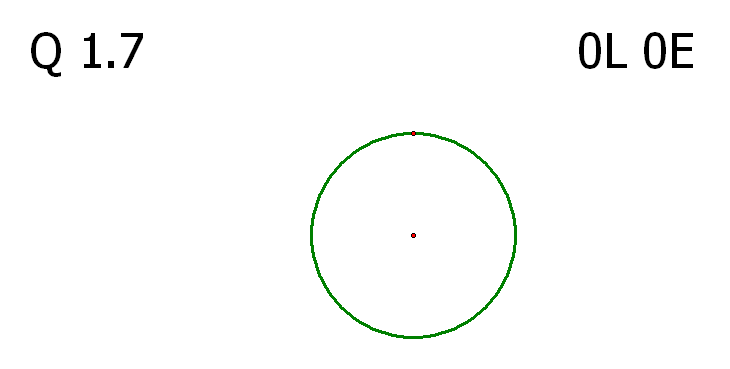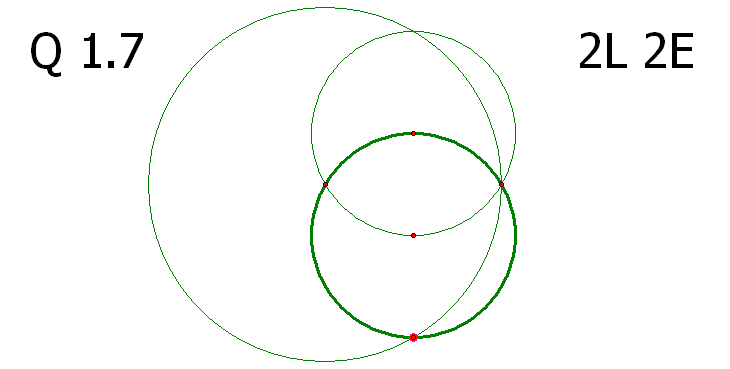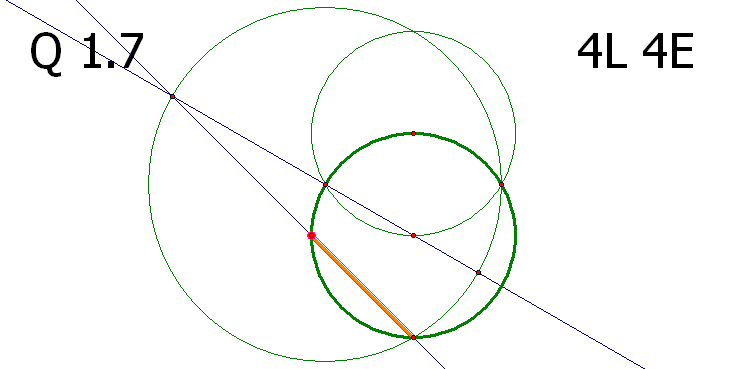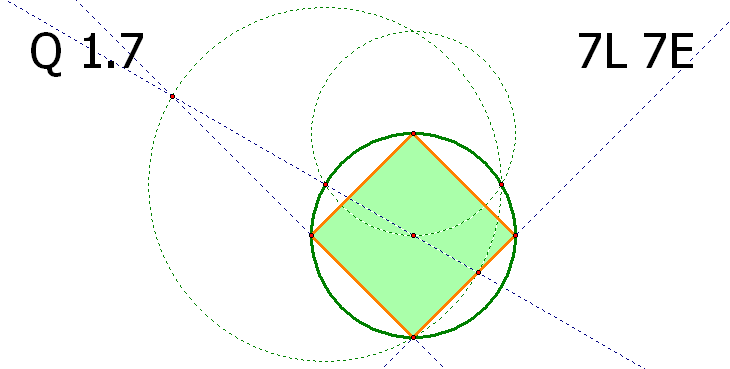
마지막 문제라고는 하지만 첫 단계인?α의 1.7의 수준이 이 정도라면
별을 다 모으려는 시도가 상당한 가시밭길인 듯 느껴지네요.
이보다 더 쉬운(1 단계에 어울릴만한) 해결책을 찾고싶지만 일단은 GG 입니다.
1.7의 E별을 획득하신 분들 중 아래의 해법과 다른 분이 계시다면
그러한 방법과 아이디어를 구경할 수 있기 바라며 풀이 과정을 올려보도록 하겠습니다.
※ 제가 만족시킨 7L 7E 해법이나 실패한 방법입니다.
왜냐하면 주어진 꼭지점을 사용하지 않은 내접 정사각형이기 때문이지요.

(이 정도가 제 한계인 듯 싶어 유투브의 모범 답안을 찾아보았더니…)
※ 유투브에 공개된 7L 7E 해법입니다.
(1단계에 어울리지 않아 보이는 어려운 풀이로 생각됩니다. 더 쉬운 풀이가 있었으면 싶은데…)

<iframe width="560" height="315" src="https://www.youtube.com/embed/fDldZy_pNQY" frameborder="0"></iframe>
심심풀이로 간단한 해설도 첨부합니다.

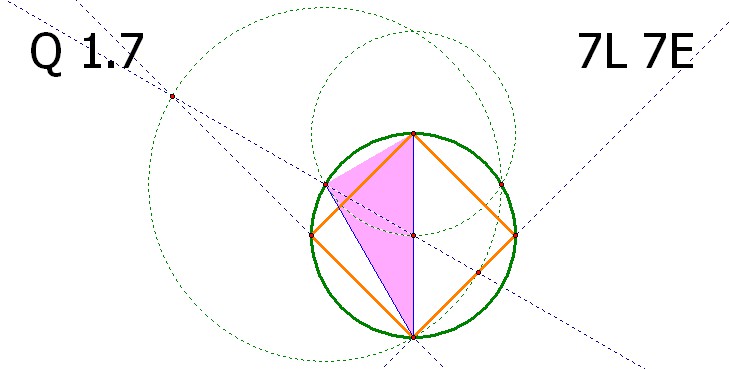
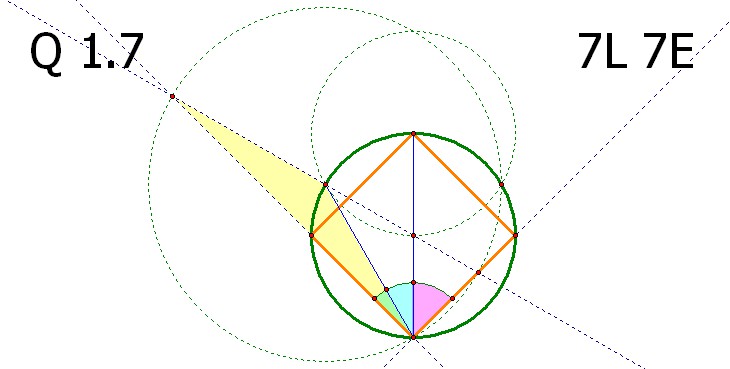
분홍 삼각형은 30도 60도 90도 로 이루어진 직각삼각형입니다.

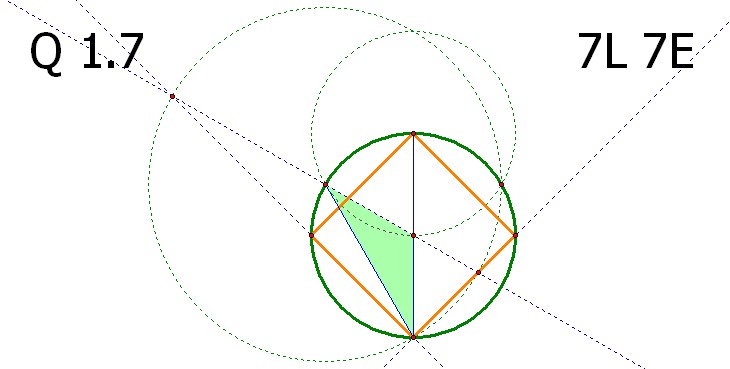
연두색 삼각형은 30도 30도 120도 로 이루어진 이등변삼각형입니다.

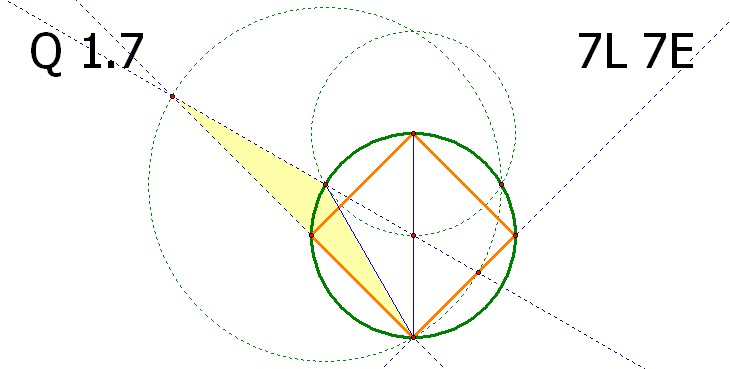
노란색 삼각형은 15도 15도 150도 로 이루어진 이등변삼각형입니다.

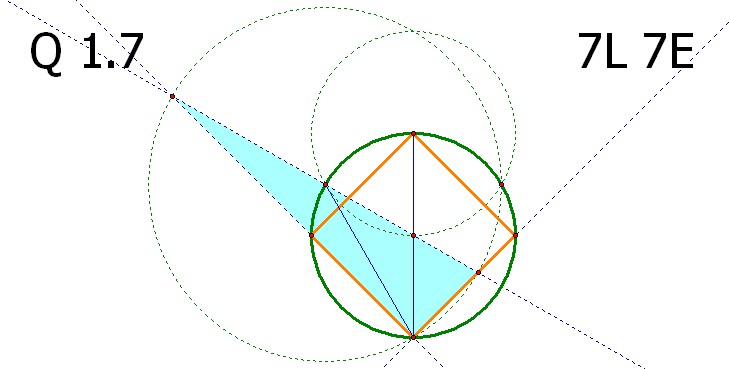
하늘색 삼각형은 가장 큰 원에 내접하는 직각삼각형 입니다.

위의 결과에 의하여 연두색 각 15도, 하늘색 각 30도, 분홍색 각 45도 가 되어 내접 정사각형이 올바르게 작도되었음이 확인됩니다.
여담으로?7L 7E 조건이지만 내접 정사각형의 네 변을 긋는 데에 4E가 소모되므로 3E만에 좌 우 두 꼭지점을 찾아야하는 압박을
심하게 받았고 결국 가장 먼저 보여드린 저의 풀이를 얻어내는 데에는 성공하였으나 주어진 꼭지점을 사용하지 않은 풀이이기 때문에
정답으로 인정받지는 못하였습니다.
그런데 모범 답안을 살펴보니 작도 과정중에 정사각형의 변을 포함하는 직선이 그어지는 것만으로 해당 변을 작도한 것으로 판정함을
알게 되어 약간의 멘붕(?)을 겪기도 하였는데요. 작도 과정 중에 목적 대상물의 일부가 포함될 경우 이를 다시 한 번 확실히 작도하여
마무리하지 않아도 되는만큼 생각을 훨씬 더 깊이 해야된다는 것을 느꼈네요. (3E만에 좌 우 두 꼭지점을 찾아야할 필요가 없었다는…)
위의 그림들은 게임 화면이 아닌 GSP 로 작도하였으며 Moving GIF 만드는 방법을 되새겨볼 겸 하여 GIF까지 만들어보았으나
간만에 해서 그런지 작도법에 대하여 고민하는 시간보다 그림 그리는 시간이 훨씬 더 걸리는 슬픈 일이 일어났네요.
해법이 궁금하신 분들에게 약간이나마 도움이 되었기를 바라며
본 문제의?7L 7E 를 위의 방법과 다르게 해결하신 분이 계시다면 그 해결 과정과 아이디어 획득에 대한
저의 궁금증도 해결될 수 있기를 기대해봅니다.
1.6의 5L 5E 해법도 고민해본 후 파악되면 이와 유사하게 만들어볼까 합니다만
다른 문제들까지 해보기에는 좀 빡세서 어찌 할지는 저도 잘 모르겠네요;;
아무튼 읽어주셔서 감사합니다.
댓글주제와 무관한 댓글, 악플은 삭제될 수 있습니다.
등록된 댓글이 없습니다.


